DIVERSITY indices : richness
12/03/2018
Glossary
Parametric methods : require specific parametric assumptions about the species abundance distribution.
Different parametric distributions may fit the observed data equally well, but lead to drastically different species richness estimates.Non-parametric methods : always obtainable and make no assumptions about the mathematical form of the underlying species abundance/incidence distributions.
Species richness : number of observed species + number of undetected species
Uniques : number of species observed in only one sampling unit
Duplicates : number of species observed in exactly two sampling units
Super-duplicates : number of species observed in at least two sampling units
Estimators of number of undetected species
Non-parametric estimators based on the information about the infrequently detected (rare) species.
1978 : Burnham & Overton
Jackknife resampling : technique especially useful to reduce the bias / variance of a biased estimator (similar to bootstrap). The basic idea with the jth order jackknife method is to consider sub-data by successively deleting j individuals from the data.
Jackknife estimator of a parameter :
- for a sample of size
n, - calculate the estimates of each n-1-sized sub-sample
- average of these calculations
Estimation of species richness :
with :
N: total number of individuals / speciesS: non-parametric maximum likelihood estimator of Ni: sampling-unit (day, trap, quadrat)t: total number of sampling unitsfr: number of individuals captured exactly r times
Clearly, S is biased and this bias decreases as t increases. Hence the following correction :
with :
j: individual / species
First-order jackknife :
(depending on unique species)
Second-order jackknife :
(depending on unique and duplicate species)


with n = t.
1987 : Chao
This method is especially useful when most of the captured individuals are caught once or twice in the sample (very small capture probabilities), for which case the kackknife estimator usually does not work well.
If there are many undetectable species, then it will be impossible to obtain a good estimate of species richness. A reliable lower bound for SR if often more practical use than an imprecise point estimate.
It is a minimum estimator of asymptotic species richness.
Chao1 estimator (number of undected species for abundance data) :

Chao2 estimator (number of undected species for incidence data) :
with :
S obs: count of the total number of species observedT: number of sampling unitsf1/Q1: uniquesf2/Q2: duplicates
1994 / 1998 : Lee & Chao, Chazdon
Incidence-based coverage estimator (ICE) :
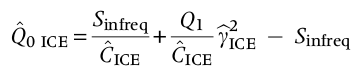 with :
with : 
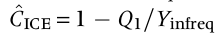
with :
Qk: number of species present inksampling unitsR: utoff frequency between infrequent and frequent species in the reference sample (= 10 as a start)S infreq: number of species occurring in fewer thanRsampling units (frequency counts for rare species)Y infreq: summed incidence frequencies for species occurring in fewer thanRsampling unitsT infreq: number of sampling units including at least one infrequent speciesC ICE: estimate of sample coveragegamma ICE: squared coefficient of variation
Models to infer species richness
1953 / 2000 : Good (& Turing)
Detection probabilities of unique species do not vary greatly among such species, so that most of the detection probabilities of uniques are concentrated at the average.
2012 : Chao (review)
Rarefaction (interpolation) : traditional method to down-sample the larger samples, when comparing the sample richnesses of different assemblages, until they are the same size
(but loss of information)Curve-fitting approaches : generally do not provide the variances of the resulting estimates
Extrapolation : use parametric curves to extrapolate a species-accumulation or species-area curve to predict its asymptote, which is used as an estimate of species richness, for hypothetical samples larger than the actual samples
(can be reliable to about twice the actual sample sizes)Curve-fitting : fit a truncated parametric distribution or functional form to the observed species abundances to obtain an estimate of species richness
Sampling-theory-based approaches : two type of sampling data :
- individual-based (abundance) data
- sample-based (incidence) data
2012 : Colwell
For sample-based incidence data :
interpolation : sample-based rarefaction (Bernoulli product model)
extrapolation : estimate of asymptotic species richness for a larger number of sampling units,
which requires an estimation of the number of undetected species :- Chao2 estimator
- ICE for assemblages with many rare species
Incidence-based models
Especially advantageous for social species (individuals difficult to distinguish and to count), and avoid the risk of double-counting individuals within sessions.
Usually require :
- Count of the total number of species observed
- Number of unique species
- Number of duplicate species
2017 : Chao
Extension of incidence-based sampling model of Colwell to encompass datasets with only :
- Count of the total number of species observed
- Number of super-duplicate species
STEPS :
- Estimate the true number of duplicates with :
- observed numbers of uniques (
S obs = S uniques + S super-duplicates) - observed numbers of super-duplicates (species observed in at least two sampling units)
- observed numbers of uniques (
- Infer the number of undected species with :
- observed numbers of uniques
- estimated number of duplicates
- Infer the species richness with :
- observed numbers of species
- estimated number of undetected species
SR estimated = S obs + S undetected
Citations
- Burnham, K., & Overton, W. (1978). Estimation of the Size of a Closed Population when Capture Probabilities vary Among Animals. Biometrika, 65(3), 625-633. https://doi.org/10.2307/2335915
- Chao, A. (1987). Estimating the Population Size for Capture-Recapture Data with Unequal Catchability. Biometrics, 43(4), 783-791. https://doi.org/10.2307/2531532
- Chao, A. & Chiu, C.-H. (2012) Estimation of species richness and shared species richness. In Methods and Applications of Statistics in the Atmospheric and Earth Sciences (ed. N. Balakrishnan), pp. 76–111, Wiley, New York, NY, USA.
- Chao, A., Colwell, R. K., Chiu, C.-H. and Townsend, D. (2017), Seen once or more than once: applying Good–Turing theory to estimate species richness using only unique observations and a species list. Methods Ecol Evol, 8: 1221–1232. https://doi.org/10.1111/2041-210X.12768
- Chazdon, Robin & Colwell, Robert & S. Denslow, J & Guariguata, Manuel. (1998). Statistical methods for estimating species richness of woody regeneration in primary and secondary rain forests of NE Costa Rica. In Forest biodiversity research, monitoring and modelling. 285-309.
- Colwell, Robert & Chao, Anne & J. Gotelli, Nicholas & Lin, SY & Mao, Chang Xuan & Chazdon, Robin & T. Longino, John. (2012). Models and estimators linking individual-based and sample-based rarefaction, extrapolation and comparison of assemblages. Journal of Plant Ecology. 5. 3-21. https://doi.org/10.1093/jpe/rtr044.
- Good, I. (1953). The Population Frequencies of Species and the Estimation of Population Parameters. Biometrika, 40(3/4), 237-264. https://doi.org/10.2307/2333344
- Lee, S., & Chao, A. (1994). Estimating Population Size Via Sample Coverage for Closed Capture-Recapture Models. Biometrics, 50(1), 88-97. https://doi.org/10.2307/2533199
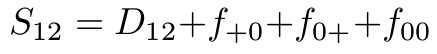
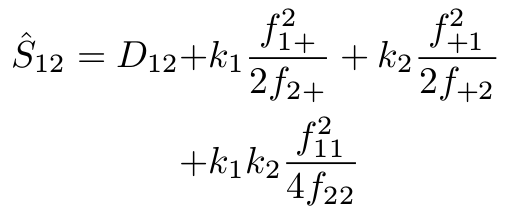 with
with 